How Do You Know if an Arc Is the Same or Half of an Inscribed Angle

The inscribed angle θ is half of the central angle 2θ that subtends the same arc on the circle. The angle θ does not alter as its vertex is moved around on the circumvolve.

In geometry, an inscribed angle is the angle formed in the interior of a circle when 2 chords intersect on the circle. Information technology can as well be defined as the angle subtended at a signal on the circle by two given points on the circumvolve.

Equivalently, an inscribed angle is defined by ii chords of the circle sharing an endpoint.

The inscribed angle theorem relates the measure of an inscribed angle to that of the primal bending subtending the same arc.

The inscribed bending theorem appears every bit Proffer 20 on Book 3 of Euclid's Elements.

Theorem [edit]

Statement [edit]

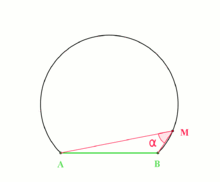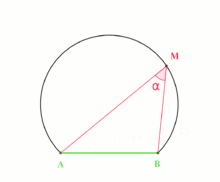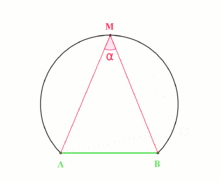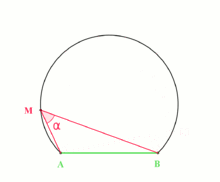
For fixed points A and B, the gear up of points M in the aeroplane for which the angle AMB is equal toα is an arc of a circle. The mensurate of ∠ AOB, where O is the center of the circle, is 2α.

The inscribed angle theorem states that an angle θ inscribed in a circumvolve is one-half of the central angle twoθ that subtends the aforementioned arc on the circle. Therefore, the angle does not modify as its vertex is moved to different positions on the circle.

Proof [edit]

Inscribed angles where one chord is a diameter [edit]

Instance: One chord is a diameter

Permit O be the middle of a circumvolve, as in the diagram at correct. Cull ii points on the circumvolve, and call them V and A. Draw line VO and extended past O so that it intersects the circle at point B which is diametrically opposite the bespeak V. Draw an bending whose vertex is point V and whose sides laissez passer through points A and B.

Draw line OA. Angle BOA is a central angle; call it θ. Lines OV and OA are both radii of the circumvolve, then they have equal lengths. Therefore, triangle VOA is isosceles, so angle BVA (the inscribed angle) and angle VAO are equal; let each of them exist denoted as ψ.

Angles BOA and AOV add upward to 180°, since line VB passing through O is a straight line. Therefore, angle AOV measures 180° −θ.

Information technology is known that the three angles of a triangle add upwards to 180°, and the three angles of triangle VOA are:

180° − θ

ψ

ψ.

Therefore,

${\displaystyle ii\psi +180^{\circ }-\theta =180^{\circ }.}$

Decrease

${\displaystyle (180^{\circ }-\theta )}$

from both sides,

${\displaystyle ii\psi =\theta ,}$

where θ is the central bending subtending arc AB and ψ is the inscribed angle subtending arc AB.

Inscribed angles with the heart of the circumvolve in their interior [edit]

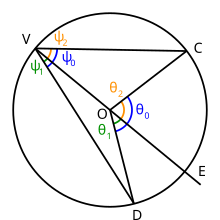
Case: Center interior to angle

Given a circle whose center is indicate O, choose three points V, C, and D on the circumvolve. Draw lines VC and VD: angle DVC is an inscribed angle. Now draw line VO and extend it past betoken O and then that it intersects the circle at point Eastward. Bending DVC subtends arc DC on the circle.

Suppose this arc includes point Due east within it. Point E is diametrically reverse to point Five. Angles DVE and EVC are as well inscribed angles, but both of these angles have ane side which passes through the center of the circle, therefore the theorem from the above Role 1 can exist applied to them.

Therefore,

${\displaystyle \angle DVC=\angle DVE+\angle EVC.}$

so allow

${\displaystyle \psi _{0}=\angle DVC,}$

${\displaystyle \psi _{1}=\angle DVE,}$

${\displaystyle \psi _{2}=\bending EVC,}$

so that

${\displaystyle \psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (one)}$

Draw lines OC and OD. Angle DOC is a primal angle, but so are angles DOE and EOC, and

${\displaystyle \angle Md=\bending DOE+\bending EOC.}$

Let

${\displaystyle \theta _{0}=\angle DOC,}$

${\displaystyle \theta _{1}=\angle DOE,}$

${\displaystyle \theta _{2}=\angle EOC,}$

so that

${\displaystyle \theta _{0}=\theta _{1}+\theta _{two}.\qquad \qquad (2)}$

From Role One we know that ${\displaystyle \theta _{1}=two\psi _{ane}}$ and that ${\displaystyle \theta _{2}=2\psi _{2}}$ . Combining these results with equation (2) yields

${\displaystyle \theta _{0}=2\psi _{1}+2\psi _{two}=2(\psi _{1}+\psi _{2})}$

therefore, by equation (one),

${\displaystyle \theta _{0}=two\psi _{0}.}$

Inscribed angles with the center of the circle in their exterior [edit]

Case: Center outside to bending

The previous case can exist extended to encompass the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the showtime part of this proof.

Given a circle whose center is point O, choose three points V, C, and D on the circle. Draw lines VC and VD: angle DVC is an inscribed angle. At present describe line VO and extend it past signal O and then that it intersects the circumvolve at point Eastward. Angle DVC subtends arc DC on the circle.

Suppose this arc does non include betoken E inside it. Point E is diametrically contrary to point V. Angles EVD and EVC are also inscribed angles, but both of these angles have one side which passes through the centre of the circle, therefore the theorem from the above Office 1 can be applied to them.

Therefore,

${\displaystyle \angle DVC=\angle EVC-\angle EVD}$ .

so let

${\displaystyle \psi _{0}=\bending DVC,}$

${\displaystyle \psi _{one}=\angle EVD,}$

${\displaystyle \psi _{two}=\angle EVC,}$

so that

${\displaystyle \psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (iii)}$

Draw lines OC and OD. Bending Doctor is a primal bending, but so are angles EOD and EOC, and

${\displaystyle \angle DOC=\angle EOC-\angle EOD.}$

Permit

${\displaystyle \theta _{0}=\bending DOC,}$

${\displaystyle \theta _{1}=\angle EOD,}$

${\displaystyle \theta _{ii}=\angle EOC,}$

so that

${\displaystyle \theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)}$

From Part One nosotros know that ${\displaystyle \theta _{1}=ii\psi _{1}}$ and that ${\displaystyle \theta _{2}=2\psi _{2}}$ . Combining these results with equation (iv) yields

${\displaystyle \theta _{0}=ii\psi _{2}-ii\psi _{1}}$

therefore, by equation (3),

${\displaystyle \theta _{0}=ii\psi _{0}.}$

Corollary [edit]

Past a similar statement, the bending between a chord and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See likewise Tangent lines to circles.

Applications [edit]

The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special instance of the theorem is Thales' theorem, which states that the angle subtended past a diameter is always ninety°, i.e., a right bending. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true tin can be inscribed in a circle. As another case, the inscribed bending theorem is the basis for several theorems related to the power of a point with respect to a circle. Further, information technology allows i to evidence that when two chords intersect in a circumvolve, the products of the lengths of their pieces are equal.

Inscribed angle theorems for ellipses, hyperbolas and parabolas [edit]

Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. The essential differences are the measurements of an bending. (An angle is considered a pair of intersecting lines.)

• Ellipse
• Hyperbola
• Parabola

References [edit]

• Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN0-486-26530-7.
• Gellert Due west, Küstner H, Hellwich M, Kästner H (1977). The VNR Curtailed Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN0-442-22646-two.
• Moise, Edwin Eastward. (1974). Elementary Geometry from an Avant-garde Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN0-201-04793-iv.

External links [edit]

• Weisstein, Eric W. "Inscribed Angle". MathWorld.
• Human relationship Between Central Bending and Inscribed Bending
• Munching on Inscribed Angles at cut-the-knot
• Arc Primal Bending With interactive animation
• Arc Peripheral (inscribed) Bending With interactive animation
• Arc Primal Bending Theorem With interactive animation
• At bookofproofs.org

wilkeforappou87.blogspot.com

Source: https://en.wikipedia.org/wiki/Inscribed_angle

Share this post